

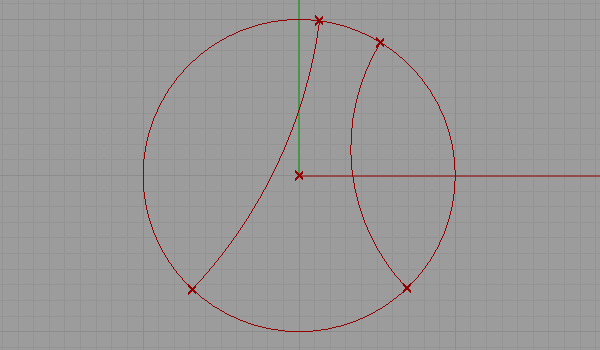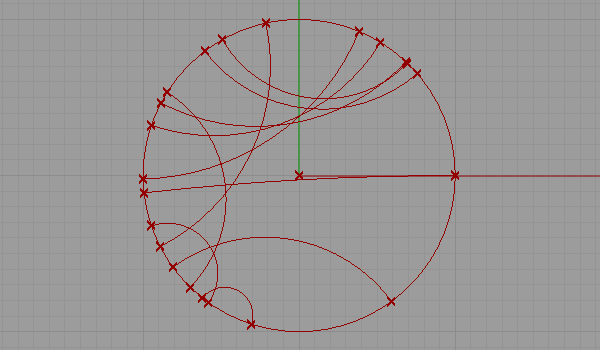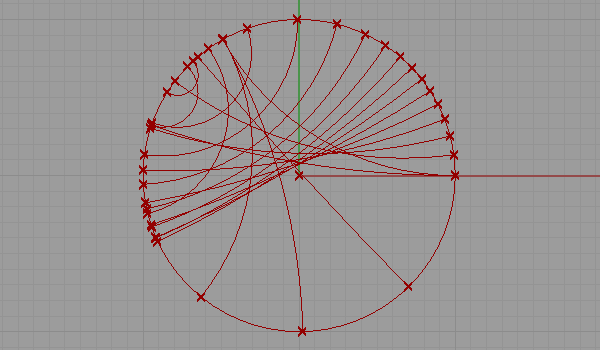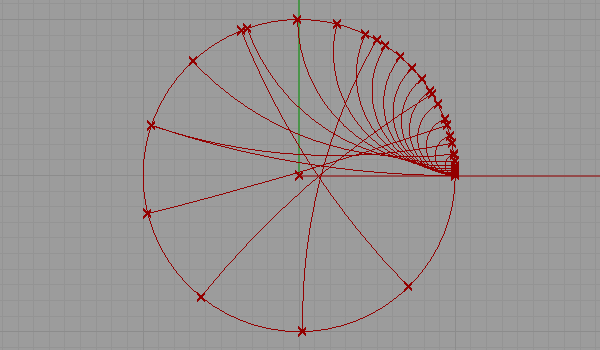
In the Poincaré case, lines are given by diameters of the circle or arcs. made the author start to investigate the development of early graph theory in the French mathematical literature. Remember that in the half-plane case, the lines were either Euclidean lines, perpendicular onto the real line, or half-circles, also perpendicular onto the real line. Moreover, every such intersection is a hyperbolic line. The subject of graph theory had its beginnings in recreational math problems ( see number game ), but it has grown into a significant area of mathematical research, with applications in chemistry, operations research, social sciences, and computer science. With a circle in the extended complex plane perpendicular to the unit circle bounding graph theory, branch of mathematics concerned with networks of points connected by lines. Just like in the half-plane model, we will look first at lines in this model.

Note that we are still in the complex plane. In geometry, the Poincar disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle. The underlying space of this model is the open unit disk Circle graph Coloring book Shape Printing, circle, angle. We note that H does indeed form a group of. Sphere Theory of relativity General relativity Poincar disk model, Geometric Measure Theory. The set D is called the hyperbolic plane, and H is called the transformation group in hyperbolic geometry. As you will see at the end of this page, it is this model that appears in Escher's work. The Poincar disk model for hyperbolic geometry is the pair (D, H) where D consists of all points z in C such that z < 1, and H consists of all Mbius transformations T for which T(D) D. You may ask yourself why is it necessary to do that? The reason is that this model is more useful, as it gives more insight and we can make a better use of the apparatus from the complex analysis. It is worth mentioning that there are also theoretical limits on the. This model is constructed starting from the previous one. One of the purposes of this paper is to clarify the strong analogy between potential theory on the open unit disk and the homogeneous tree, to which we dedicate an introductory section. The second model that we use to represent the hyperbolic plane is called the Poincaré disk model, named after the great French mathematician, Henri Poincaré (1854 - 1912). The Poincaré disk model for the hyperbolic plane In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent.The Poincaré model for the hyperbolic plane, Section 7ħ. For Euler number in 3-manifold topology, see Seifert fiber space. For Euler characteristic class, see Euler class. The metric is which makes identical objects appear exponentially smaller as they approach the boundary. This article is about Euler characteristic number. dimensions, we will largely use the Poincar disk model.


 0 kommentar(er)
0 kommentar(er)
